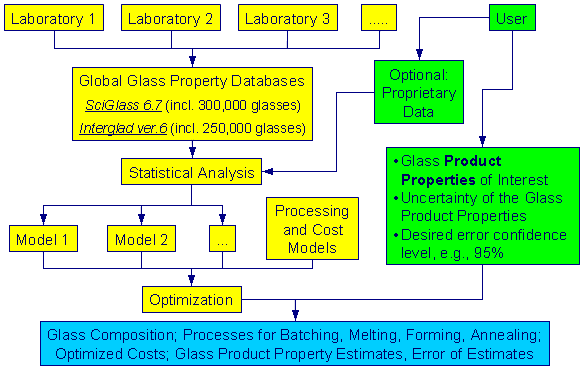
Optimization (Reversed Glass Modeling)

Once several reliable glass models are established, it is possible to combine and reverse the calculations, e.g., to determine the optimal glass composition from the desired properties. Besides the property-composition models on this website other functions can also be considered in the optimization procedure such as financial estimators or processing calculations. Reversed modeling allows influencing selectively the desired glass property without affecting other properties, the production costs, or energy consumption significantly. It simultaneously allows calculation of the optimal process parameters for all processes considered in the model. The importance of the parameters can be weighted differently as described by Huff & Call (1973).
An interesting and still rather uncomplicated application of reversed modeling combines property-composition relations for the viscosity curve, in particular for the forming temperature, with functions for the liquidus temperature. If the difference between the forming and liquidus temperatures is optimized, without influencing other properties significantly, it is possible to reduce energy consumption during glass melting and cooling as shown in a recently published article by Wallenberger & Hicks (2006).
For demonstration a simple calculator may be downloaded here. It combines models for the liquidus temperature, viscosity curve, thermal expansion, and the cost of raw materials for soda-lime-silica glasses.
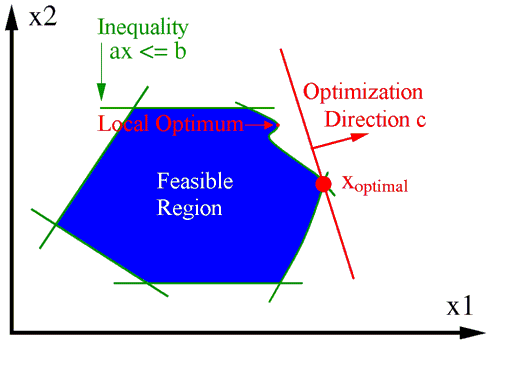
For reversed glass modeling common linear optimization procedures may not always be applicable because local optima can differ from the global optimum as seen in the figure below. In this case, non-convex optimization techniques should be used, e.g., a brute-force search. Huff & Call (1973) used random and simplex pattern search procedures.
At present, the computational fluid dynamics (CFD) approach to furnace modeling combines some of the glass models mentioned above, however, many glass properties are still insufficiently investigated experimentally and statistically. These properties include batch melting kinetics, melt density, surface tension, thermal conductivity, transmission spectra, gas solubilities, evaporation behavior, and tank corrosion, to mention just a few. The design of an efficient optimization algorithm requires co-operation of several institutions.

Wikipedia gives a general overview abount optimization in mathematics. Optimization is part of the so-called Six Sigma operations improvement in the industry.

Optimization by the Solver-Tool in Microsoft Excel:
1) Listing of the desired properties;
2) Entering of all required models, e.g., for the reliable calculation of properties based on the glass composition, including a formula for estimating the production costs;
3) Calculation of the squares of the differences (errors) between desired and calculated properties;
4) Reduction of the sum of square errors using the Solver-Tool in Microsoft Excel with the glass components or process parameters as variables.

Huff & Call (1973)
N. T. Huff, A. D. Call: "Computerized Prediction of Glass Compositions from Properties"; J. Am. Ceram. Soc., vol. 56, no. 2, 1973, p 55-57.

Wallenberger & Hicks (2006)
F. T. Wallenberger & R. J. Hicks: "The effect of boron on the properties of fibreglass melts"; Glass Technol.: Europ. J. Glass Sci. Technol. A, vol. 47, no. 5, 2006, p 148-152.