On this page statistical analysis for the calculation of glass properties is explained (see also overview article at Wikipedia). The topic may be divided as follows:
1) Linear regression,
2) Non-linear regression,
3) Special applications.


1) Linear regression
Linear regression is characterized by liniarity in the coefficients. However, the equation does not need to be linear in the variables such as seen in Figure 1 and described in a linear regression tutorial (PDF, 0.4 MB).

Figure 1: Linear regression according to the equation z = a + b·x + c·x² + d·x³ + e·y + f·y² + g·y³.
The equation is linear in the coefficients a, b, c, d, e, f, and g, but not linear in the variables x and y.

It is possible to desribe almost all glass properties using linear regression, except liquidus temperatures, phase separation, and specialized chemical durability tests such as vapor hydration. For further information it is referred to the linear regression tutorial (PDF, 0.4 MB).


2) Non-linear regression
Glass liquidus temperatures can be modeled using disconnected peak functions. For the sake of simplicity as peak function second order polynomials are explained here, but in principle other functions such as Gauss curves or superimposed step-functions ("neurons") as used for neural networks can be applied as well. The peak functions can be based on the quadratic equation that may be expressed two-dimensionally as y = ax² + bx + c with the coefficient a being negative or zero and without any limitations for the coefficients b and c. The independent variable x is substituted by the component concentration in a binary glass and y represents the liquidus temperature in °C. For the reason that a large number of experimental data is available in binary silicate glass systems in some cases cubic equations may be used for modeling. In multi-component systems the two-dimensional quadratic equation must be extended to the level of dimensions that equals the number of components in the glass. Several disconnected peak functions are fitted to the liquidus surface ("landscape") by non-linear regression, for example using the Solver tool in Microsoft Excel. The results of the individual functions are not added, but only the maximum of all functions is counted as response, thereby enabling sharp eutectic minima:

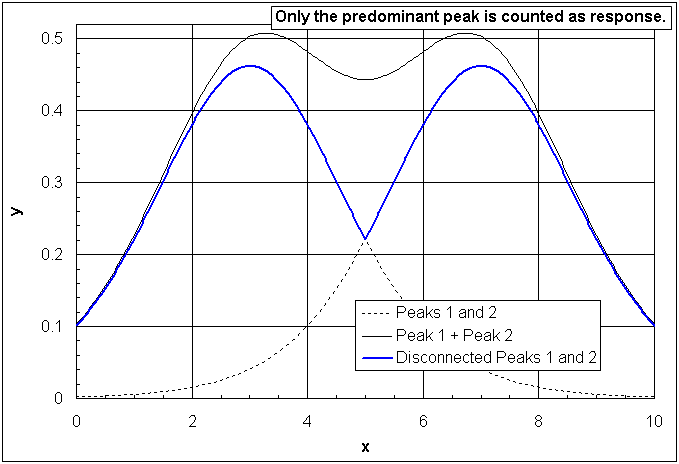
Figure 2: Principle of disconnected peak functions.

Figures 3 to 5 show the application of disconnected peak functions to liquidus temperature modeling in the ternary system SiO₂-Na₂O-CaO based on 237 experimental data from 28 investigators, extracted from SciGlass:

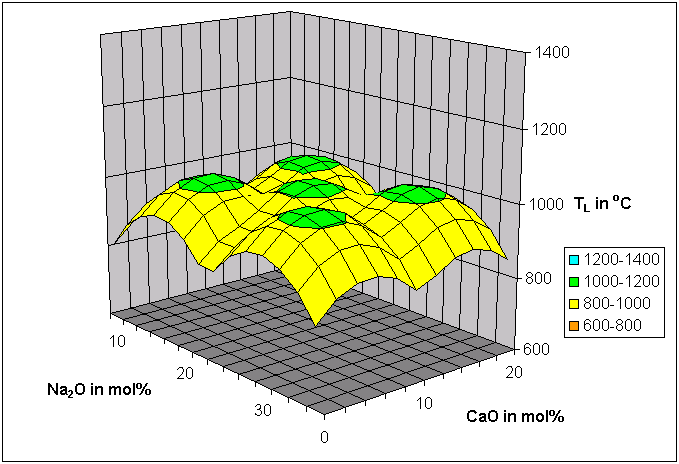
Figure 3: Model initiation, peaks distributed evenly in composition space, R² = 0.09.


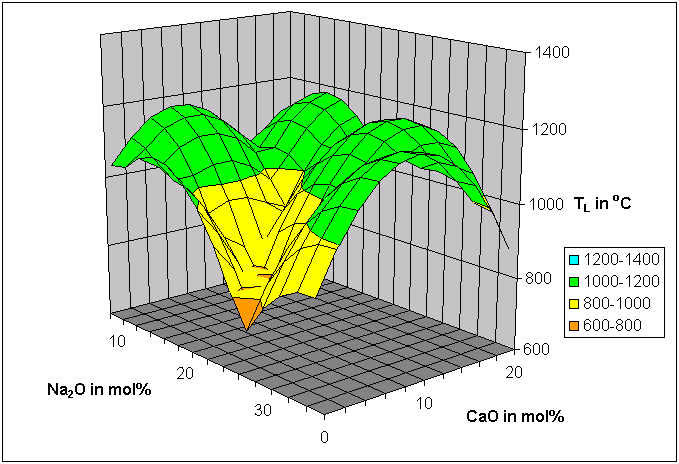
Figure 4: The peak functions are allowed to move, R² = 0.83.


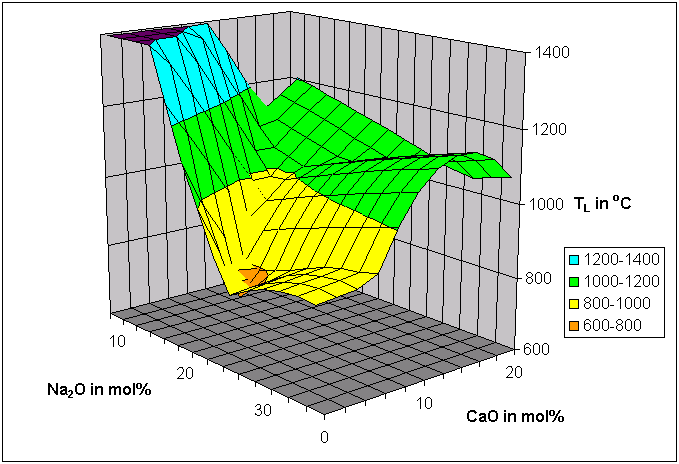
Figure 5: Final liquidus surface in the system SiO₂-Na₂O-CaO, R² = 0.985, Error = 15°C.

More information about disconnected peak functions and their application to liquidus temperatures modeling in the six-component system SiO2-Na2O-CaO-Al2O3-MgO-K2O can be found in the proceeding: A. Fluegel: "Modeling of glass liquidus temperatures using disconnected peak functions"; Presentation at ACerS 2007 Glass and Optical Materials Division Meeting, Rochester, NY, USA.


3) Special applications
Statistical analysis may be applied to thermodynamic glass modeling using chemical equilibrium constants as coefficients.
Another special application represents variable database search modeling, where the model is automatically derived from similar glass compositions in a (possibly proprietary) database. For more information please use the contact page.